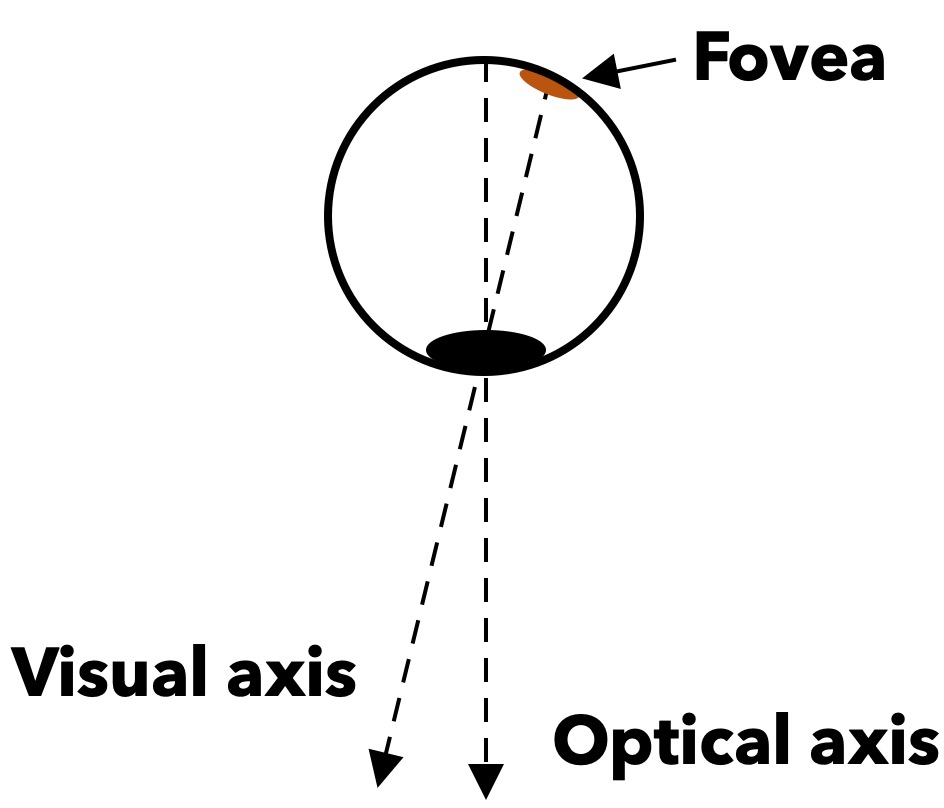
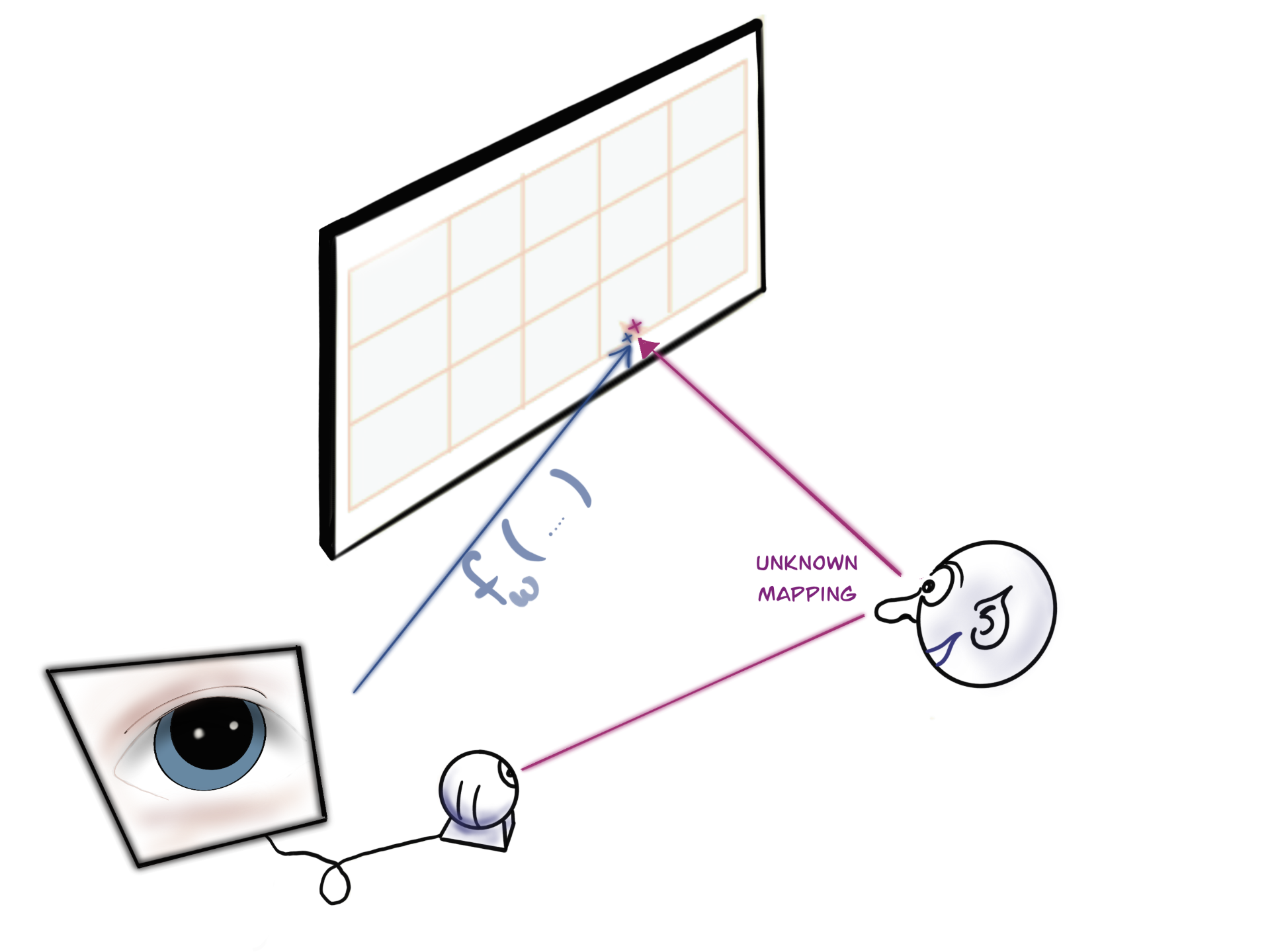
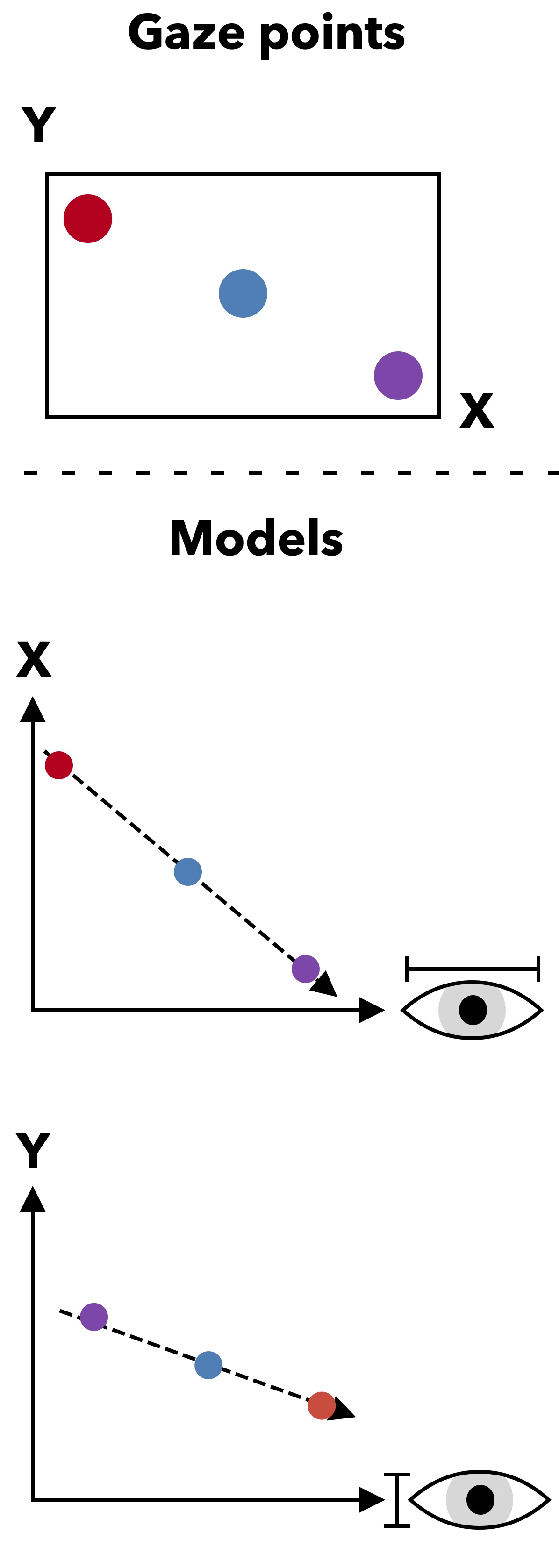
This is the first mandatory assignment in which you will implement a regression model to estimate where a person is looking (this is known as gaze) from images of eyes.
You only have to hand in this Jupyter Notebook containing your implementation and notes (markdown or python cells), see the bottom of this page for handin details. For the TA's to assess the assignment we kindly ask you to also hand in the data
folder. If you are not comfortable sharing your data with the TA's leave that folder out for the handin, but provide the plots for assessment. Refer to the bottom of the page for submission details.
Before you start solving the assignment, carefully read through the entire assignment to get an overview of the problem and the tasks.
Notice that the optional Task 23 and onward relates to exercises in next week. You may save some time by postponing it until then.
Important! Complete all tasks marked with high (red) priority before attempting to solve the others, as they are optional. Optional tasks and further analysis can help improve results, but feel free to explore methods and data as you choose.