Linear Algebra

This tutorial will cover basic terms in linear algebra and their implementation in NumPy. The tutorial includes:

  1. Data structures in linear algebra
  2. Vectors operations (addition , inner product, length vs number of elements ...)
  3. Matrix operations
  4. Special matrices
  5. Determinant and inverse of a matrix

Data structures in linear algebra

Define:

  • Scalar: Single number
  • Vector: Array of numbers
  • Matrix: 2-dimensional array of numbers
  • Tensor: $n$-dimensional array of numbers where $n > 2$

NumPy represents a vector as a 1-D array, a matrix as a 2-D array (array of arrays), and an $n$-tensor as a $n$-dimensional array (e.g. A 3D-tensor is an array of 2D arrays etc.):

Figure 1

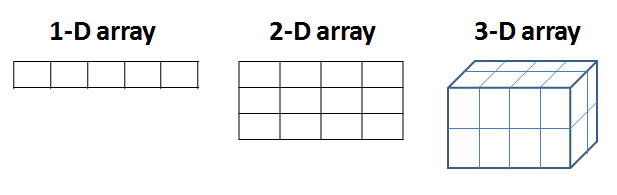
The following cells demonstrates how to create Numpy arrays:

#import the numpy lib
import numpy as np
#Vector with 4 elements:
a = np.array([1, 6, 3, 1])
print(a)
[1 6 3 1]

# A 2x4 matrix:
A = np.array([[1, 42, 6, 4], [2, 6, 87, 2]])
print(A)
[[ 1 42  6  4]
 [ 2  6 87  2]]

#print the size of the matrix
print(A.shape)
(2, 4)

# A 2x2x4 tensor:
T = np.array([[[1, 23, 3, 4], [42, 6, 7, 87]], [[9, 3, 11, 2], [2, 22, 15, 101]]])
print(T)
[[[  1  23   3   4]
  [ 42   6   7  87]]

 [[  9   3  11   2]
  [  2  22  15 101]]]

#print the size of the tensor
print(T.shape)
(2, 2, 4)

Vector Operations

A vector multiplied by a scalar: 

a = np.array([3, 22, 3, 21])
a * 2

dot product/ inner product: The dot product (see lecture slides for details) of vectors $a$ and $b$ with $n$ elements each:

$$ a\cdot b =\sum_i^N a_ib_i = a^\top b $$

The dot product can be calculated using the Numpy function np.dot(a,b) : 

#Create 2 vectors v1 and b
a = np.array([1, 2, 3, 42])
b = np.array([2, 3, 4, 5])
# calculate the dot product
np.dot(a, b)

Summation and Subtraction of 2 vectors: Elementwise summation/subtraction/multiplication

Note

The elementwise operations also exist for matrices and tensors. 

#create 2 vectors
a = np.array([1, 2, 3, 42])
b = np.array([2, 3, 4, 5])

print("a + b is : \n", a + b)
print("a - b is :  \n", a - b)
print("a * b is :  \n", a * b)

Length and dimensionality of vectors

The Euclidean distance ($L2$-norm) of a vector $a$ is the square root of the inner product $$ |a| =\sqrt{\sum_i^N a_i^2 }= \sqrt{a^\top a} $$ .

# inner product of v1 with itself
a_a_inner_product = np.dot(a, a)
Euc_len_a = np.sqrt(a_a_inner_product)
print('Euclidean distance of v1:', Euc_len_a)

The Euclidean length can also be determined by a single built-in numpy function np.linalg.norm() 

print('Euclidean distance of v1:', np.linalg.norm(a))

Orthogonal and normal vectors

Vectors $a$ and $b$ are considered orthogonal/perpendicular if $ a^\top b=0$.

Recall

Recall that the dot product is related to the angle between vectors $a$ and $b$:

$$ \cos(\theta) = \frac{a \cdot b}{\|a\| \|b\|} $$ 
# Orthognonal vectors
a = np.array([1, -2, 4])
b = np.array([2, 5, 2])

print(a.dot(b))  ## Alternative way to do dot product. Equivalent to (np.dot(a,b))
0

Orthonormal vectors: Defined as two orthogonal vectors both with unit length.

In the cell below, orthogonal vectors a and b are normalized by division with their length. 

a_normalized = a / np.linalg.norm(a)
print('a_normalized:', a_normalized)
b_normalized = b / np.linalg.norm(b)
print('b_normalized:', b_normalized)

#inner product of orthonormal vectors
print('inner product of a_normalized and b_normalized: \n', a_normalized.dot(b_normalized))
a_normalized: [ 0.21821789 -0.43643578  0.87287156]
b_normalized: [0.34815531 0.87038828 0.34815531]
inner product of a_normalized and b_normalized: 
 0.0

Matrix Operations

The following section provides an overview of important matrix properties and well-known matrix compositions.

Square matrix: A two-dimensional array with the same number of rows and columns.

A = np.random.randint(5, size=(3, 3))
A

Identity matrix is a square matrix that contains ones on the diagonal and zeros elsewhere.

The NumPy function np.identity(N) creates an identity matrix with N elements on the diagonal. 

I3 = np.identity(3)
I3
I4 = np.identity(4)
I4

Diagonal matrix: A diagonal matrix is a matrix with non-zero elements in the diagonal and zeroes elsewhere.

The NumPy function np.diag(a) creates a 2D array (diagonal matrix) given a 1D array (list/vector containing diagonal elements) as input. 

# Create an array:
v = np.array([3., 2., 5.])
# Create a matrix with elements of v on the diagonal:
D = np.diag(v)
print(D)

Matrix multiplication

Matrix multiplication of two matrices consist of inner products of row-column pairs:

Consider the matrices A1 and A2:

A1 = np.array([[1, 3, 0], [4, 4, 4]])
A2 = np.array([[2, 2], [0, 4], [2, 3]])
Tip

In Numpy, matrices (and other arrays) are zero-indexed like regular Python lists. This is in contrast to mathematical notation, which is one-indexed.

In the following, we demonstrate matrix multiplication as a series of inner products. The cell below shows matrix multiplication of A1 and A2 using the dot function in Numpy: 

np.dot(A1, A2)

The first element ($2$) of the result is calculated as the inner product of the first row of A1 and the first column of A2 :

#A1 first row, A2 first column : position [1,1]
np.dot(A1[0, :], A2[:, 0])

Similarly, the other elements can be calculated using the appropriate combinations of rows A1 and columns in A2 : 

#A1 second row, A2 first column : position [2,1]
print("A1 second row, A2 first column:", np.dot(A1[1, :], A2[:, 0]))

#A1 first row, A2 second column : position [1,2]
print("A1 first row, A2 second column:", np.dot(A1[0, :], A2[:, 1]))

#A1 second row, A2 second column : position [2,2]
print("A1 second row, A2 second column:", np.dot(A1[1, :], A2[:, 1]))
A1 second row, A2 first column: 16
A1 first row, A2 second column: 14
A1 second row, A2 second column: 36

Identity matrix

Multiplying a matrix A (from either left or right) with the identity matrix yields the matrix A. Thus, $$ AI = A = IA. $$ An example is provided below:

# create 3x3 matrix A with random values between 0 and 4.
A = np.random.randint(5, size=(3, 3))

# create 3x3 identity matrix.
I = np.identity(3)

# multiply the matrices
R = np.dot(A, I)

print("A:\n", A, "\nI:\n", I, "\nmultiplication result:\n", R)
A:
 [[0 4 3]
 [1 1 1]
 [4 4 4]] 
I:
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]] 
multiplication result:
 [[0. 4. 3.]
 [1. 1. 1.]
 [4. 4. 4.]]

Determinant and inverse of a matrix

We use np.linalg.det() to get determinant of a matrix. 

# example matrices
A = np.array([[1, 1, 1], [0, 2, 5], [2, 5, -1]])
B = np.array([[0, 0, 0], [0, 2, 5], [2, 5, -1]])

# calculate the determinant 
print("det(A):", np.linalg.det(A))
print("det(B):", np.linalg.det(B))
det(A): -21.0
det(B): 0.0

The function np.linalg.inv(A) can be used to calculate the inverse of a matrix.

Note

The function returns an error when the matrix is singular (i.e. the determinant is zero).

print("A^-1:", np.linalg.inv(A))
print("B^-1:", np.linalg.inv(B))  # This yields an error because B is singular
A^-1: [[ 1.28571429 -0.28571429 -0.14285714]
 [-0.47619048  0.14285714  0.23809524]
 [ 0.19047619  0.14285714 -0.0952381 ]]

The matrix A multiplied by its inverse yields the identity matrix:

np.dot(A, np.linalg.inv(A))
Note

The result of the calculation above may be slightly off. This is due to the limitations of floating point numbers.

Diagonal matrices (determinant and inversion)

# Create a diagonal matrix 
A = np.diag([5, 2, 3])
A

The determinant of a diagonal matrix is the product of the elements on the diagonal. 

np.linalg.det(A)

The inverse of a diagonal matrix is the reciprocal of each element on the diagonal.

np.linalg.inv(A)

This concludes the tutorial.